Dennis Hollingsworth

Penrose on Consciousness, Truth, Morality and Beauty

I'd like to make a list of thinkers who are not usually constrained by their discipline Today, the list starts with Roger Penrose, then Richard Feynman...

Well, not many folks that I can add to the list at the moment.

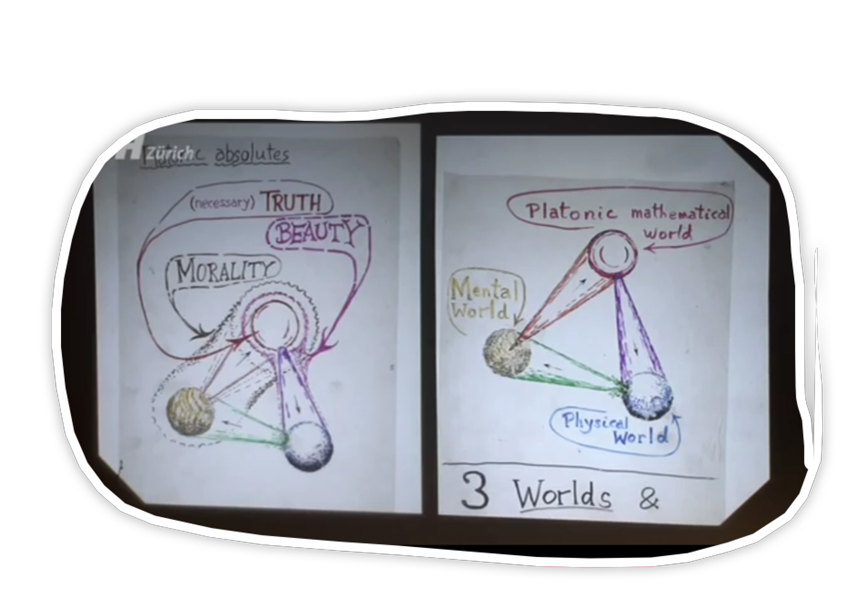
Penrose gave a lecture a couple of years ago in Zürich, you can see it here, or below the fold. In this presentation, Roger Penrose is searching for clues to the basis of consciousness, in this presentation, he traces the current extents of our understanding of this ultimate subject to the limit. Penrose eventually presents in this talk, a schematic structure of the world at large, a world itself composed of three worlds, three mysteries: the physical, mental and Platonic (which the latter is too, tripartite: Truth, Beauty and Morality)

Time = 0:51:30, Penrose introduces to the "3 Worlds & 3 Mysteries"

He returns to this theme at Time = 1:08:00

In his presentation, he brings in quantum physics, Heisenberg's Uncertainty Principal, the limits of computation and the larger realm of mathematical truth, among many other issues. Between the two moments in the video time tagged above, Penrose introduces the recent discovery of microtubules within neurons which are so small as to provides a space for quantum effects to take place.

...one of the things that one keeps finding in research and mathematics and physics at a particularly at the deep level where mathematics tends to come in at relatively profound ways, and this is, the beauty of the subject. So I have here, gone a little outside of my area and [I talk] about the other Platonic absolutes.

You see, this world has to do with truth, this has to do with absolute truth, the absolute truth that you find in mathematics, which has a sort of more absolute nature that you tend to find in other areas, but there are these other Platonic qualities, not necessarily the Truth, which is indicated by this part [referring to his diagram] but Beauty, particularly the beauty that one finds in physical laws or how mathematics applies to it, there is often beauty which is mathematical, but so often, more than not, you find that the -laws that apply to the world involve, in a deep way, this Beauty.

The final thing, which in fact is what Plato regarded the most highly, which was the morality or The Good. And this is clearly tied up with mentality, because if you want to talk about something, some act being good in some sense, it usually refers to animate creatures, human beings, not just human beings certainly... so the idea of morality is very much tied up with this side of the picture....

it does seem to me that it's not just the Truth that you find in this world the Platonic Absolute which is relevant in this picture, that these others that the quality of Beauty which has to do with these physical laws that describe the world in the incredible way...and Morality, which has to do with Mentality

Does abstract art describe this Platonic tripartite of tripartite mysterious worlds? Not necessarily (and it's not that devotees of abstraction always make this promise, see Chris Martin's recent Everything is Finished Nothing is Dead: An Article About Abstract Painting)
, it merely steers us toward Truth and Beauty, on a path that promises to be shorn as much as possible of mimesis. Does verisimilitude get a bum rap in Plato's book because representation is an artifact solely of the Mental World, and therefore can keep us from properly apprehending the Platonic realm? Yes of course, this is the point of the Allegory of the Cave. The problem for the allegory is that we, as prisoners, are denied freedom in this life, this existence. The chains never come off while we are alive at least. The best we can do is
to try to make mental leaps like this: 4th Dimension explained.

PS: Another thinker who has drawn the dotted lines which anticipate the Platonic World would be Kurt Gödel. Mathematical fan Gary Geck has dramatized a reading of Gödel's undelivered 1961 lecture: The Modern Development Of The Foundations Of Mathematics In The Light Of Philosophy